|
Size: 190
Comment:
|
← Revision 11 as of 2020-01-26 17:57:47 ⇥
Size: 1232
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| SemiAlgebraicSets are geometric shapes (sets of points) that constrained by a set of polynomial constraints. | From MathWorld we have the following definition: |
| Line 3: | Line 3: |
| A bump could be defined as follows: | A Semi Algebraic Set is a subset of $$R^n$$ which is a finite Boolean combination of sets of the form $$\{\overline{x} : f(\overline{x})>0\}$$ and $$\{\overline{x} : g(\overline{x})=0\}$$ where $$f,g \in R[X_1,X_2,...,X_n]$$ and $$\overline{x} = x_1,x_2,...,x_n$$. |
| Line 5: | Line 6: |
| bump(i,x,y) :- i=1, y+x^2-3<0, y>0. | |
| Line 7: | Line 7: |
| "Several authors have suggested using first-order logic over the real numbers to describe spatial database applications. Geometric objects are then described by polynomial inequalities with integer coefficients involving the coordinates of the objects. '''Such geometric objects are called semi-algebraic sets.'''" (Ref: [https://www.scotnpatti.com/webfiles/PhDResearch/FirstOrderBooleanAlgebraWithCardinalityConstraints/p68-dumortier.pdf On the Decidability of Semi-Linearity for Semi-Algebraic Sets and its Implications for Spatial Databases]) Thus SemiAlgebraicSets are geometric shapes (sets of points) constrained by a set of integer coefficient polynomial constraints. Example: A bump could be defined as follows: bump(i,x,y) :- i=1, y+x^2-3<=0, y>=0. Bumb would then be the set of points contained in the geometric shape below: {{attachment:bump.gif}} '''See Also SemiLinearSets''' |
From MathWorld we have the following definition:
A Semi Algebraic Set is a subset of $$R^n$$ which is a finite Boolean combination of sets of the form $$\{\overline{x} : f(\overline{x})>0\}$$ and $$\{\overline{x} : g(\overline{x})=0\}$$ where $$f,g \in R[X_1,X_2,...,X_n]$$ and $$\overline{x} = x_1,x_2,...,x_n$$.
"Several authors have suggested using first-order logic over the real numbers to describe spatial database applications. Geometric objects are then described by polynomial inequalities with integer coefficients involving the coordinates of the objects. Such geometric objects are called semi-algebraic sets." (Ref: [https://www.scotnpatti.com/webfiles/PhDResearch/FirstOrderBooleanAlgebraWithCardinalityConstraints/p68-dumortier.pdf On the Decidability of Semi-Linearity for Semi-Algebraic Sets and its Implications for Spatial Databases])
Thus SemiAlgebraicSets are geometric shapes (sets of points) constrained by a set of integer coefficient polynomial constraints.
Example: A bump could be defined as follows:
bump(i,x,y) :- i=1, y+x^2-3<=0, y>=0.
Bumb would then be the set of points contained in the geometric shape below:
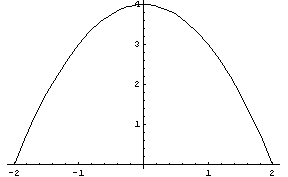
See Also SemiLinearSets
