|
Size: 15969
Comment:
|
Size: 14333
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 116: | Line 116: |
| {{{#!latex \usepackage{amsmath} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{graphicx}% \usepackage{geometry} \setcounter{MaxMatrixCols}{30} %TCIDATA{OutputFilter=latex2.dll} %TCIDATA{Version=5.00.0.2552} %TCIDATA{CSTFile=40 LaTeX article.cst} %TCIDATA{Created=Sunday, January 22, 2006 11:48:30} %TCIDATA{LastRevised=Sunday, January 22, 2006 17:58:32} %TCIDATA{<META NAME="GraphicsSave" CONTENT="32">} %TCIDATA{<META NAME="SaveForMode" CONTENT="1">} %TCIDATA{<META NAME="DocumentShell" CONTENT="Standard LaTeX\Blank - Standard LaTeX Article">} \newtheorem{theorem}{Theorem} \newtheorem{acknowledgement}[theorem]{Acknowledgement} \newtheorem{algorithm}[theorem]{Algorithm} \newtheorem{axiom}[theorem]{Axiom} \newtheorem{case}[theorem]{Case} \newtheorem{claim}[theorem]{Claim} \newtheorem{conclusion}[theorem]{Conclusion} \newtheorem{condition}[theorem]{Condition} \newtheorem{conjecture}[theorem]{Conjecture} \newtheorem{corollary}[theorem]{Corollary} \newtheorem{criterion}[theorem]{Criterion} \newtheorem{definition}[theorem]{Definition} \newtheorem{example}[theorem]{Example} \newtheorem{exercise}[theorem]{Exercise} \newtheorem{lemma}[theorem]{Lemma} \newtheorem{notation}[theorem]{Notation} \newtheorem{problem}[theorem]{Problem} \newtheorem{proposition}[theorem]{Proposition} \newtheorem{remark}[theorem]{Remark} \newtheorem{solution}[theorem]{Solution} \newtheorem{summary}[theorem]{Summary} \newenvironment{proof}[1][Proof]{\noindent\textbf{#1.} }{\ \rule{0.5em}{0.5em}} \geometry{left=0.5in,right=0.5in,top=0.5in,bottom=0.5in} %%end-prologue%% Given a user query $q$ and a document $d_{j}$ in the collection, the probabilistic model tries to estimate the probability that the user will find teh document interesting (i.e. relevant). The model assumes that this probability of relevance depends on the query and the document representations only. Further, the model assumes that there is a subset of all documents which the user prefers as the answer set for the query $q$. Such an ideal answer set is labeled $R$ and should maximized the overall probability of relevance to the user. Documents in the set $R$ are predicted to be relevant to the query. Documents not in this set are predicted to be \emph{non-relevant}. Given a query $q$, the probabilistic model assigns to each document $d_{j}$, as a measure of its similarity to the query, the ratio: \begin{equation} sim(d_{j},q) = \frac{P(d_{j}~relevant-to~q)}{P(d_{j}~non-relevant-to~q)}% \end{equation} which computes the odds of the document $d_{j}$ being relevant to the query $q$. Taking the odds of relevanceas the rank minimizes the probability of an erroneous judgement. \begin{definition} For the probabilistic mode, the index term weight variables are all binary i.e., $w_{i,j} \in{0,1}$, $w_{i,q} \in{0,1}$. A query $q$ is a subset of index terms. Let $R$ be the set of documents known (or \emph{initially guessed}) to be relevant. Let $\bar{R}$ be the complement of $R$ (i.e. the set of initially guessed \emph{non-relevant documents}). Let $P(R|\vec{d}% _{j})$ be the probability that the document $d_{j}$ is relevant to the query $q$ and $P(\bar{R}|\vec{d_{j}}$ be the probability that $d_{j}$ is non-relevant to $q$. The similarity $sim(d_{j},q)$ of the document $d_{j}$ to the query $q$ is defined as the ratio: \begin{equation} sim(d_{j},q) = \frac{ P(R|\vec{d_{j}}) }{ P(\bar{R}|\vec{d}_{j}) }% \end{equation} |
Given a user query $$q$$ and a document $$d_{j}$$ in the collection, the probabilistic model tries to estimate the probability that the user will find teh document interesting (i.e. relevant). The model assumes that this probability of relevance depends on the query and the document representations only. Further, the model assumes that there is a subset of all documents which the user prefers as the answer set for the query $$q$$. Such an ideal answer set is labeled $$R$$ and should maximized the overall probability of relevance to the user. Documents in the set $$R$$ are predicted to be relevant to the query. Documents not in this set are predicted to be ''non-relevant''. Given a query $$q$$, the probabilistic model assigns to each document $$d_{j}$$, as a measure of its similarity to the query, the ratio: $$$sim(d_{j},q) = \frac{P(d_{j}~relevant-to~q)}{P(d_{j}~non-relevant-to~q)}$$$ which computes the odds of the document $$d_{j}$$ being relevant to the query $$q$$. Taking the odds of relevance as the rank minimizes the probability of an erroneous judgement. '''Definition''' For the probabilistic mode, the index term weight variables are all binary i.e., $$w_{i,j} \in{0,1}$$, $$w_{i,q} \in{0,1}$$. A query $$q$$ is a subset of index terms. Let $$R$$ be the set of documents known (or ''initially guessed''}) to be relevant. Let $$\bar{R}$$ be the complement of $$R$$ (i.e. the set of initially guessed ''non-relevant documents''). Let $$P(R|\vec{d}_{j})$$ be the probability that the document $$d_{j}$$ is relevant to the query $$q$$ and $$P(\bar{R}|\vec{d_{j}}$$ be the probability that $$d_{j}$$ is non-relevant to $$q$$. The similarity $$sim(d_{j},q)$$ of the document $$d_{j}$$ to the query $q$ is defined as the ratio: $$$sim(d_{j},q) = \frac{ P(R|\vec{d_{j}}) }{ P(\bar{R}|\vec{d}_{j}) }$$$ |
Chapter 1 + Section 2.1 Introduction
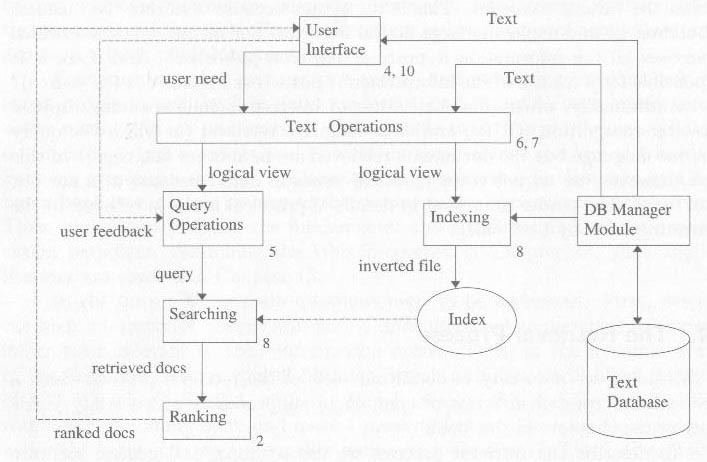
Information Retrieval Process
- Three Models of Browsing
- Flag
- Structure guided
- Hypertext
Section 2.2 A taxonomy of Information Retrieval Models
Predicting which documents are relevant is usaually dependent on a ranking algorithm.
- The three classic models in information retreival are:
Boolean Model: In the boolean model documents and queries are represented as sets of index terms, thus we say this model is a set theoretic model
Vector Model: In the vector model documents and queries are represented as vectors in a t-dimensional space, thus we say that the model is algebraic.
Probabilistic Model: The framework for modeling document and query representations is based on probability theory, and thus we sat that the model is prababilistic.
Section 2.3 Retrieval: Ad hoc and Filtering
The following is the formal definition for IR from MIR p 23.
Definition An information retrieval model is a quadruple $$D,Q,F,R(q_i , d_j))$$ where
$$D$$ is a set composed of logical views (or representations) for the documents in the collection.
$$Q$$ is a set composed of logical views (or representations) for the user information needs. Such representations are called queries
$$F$$ is a framework for modeling document representations, queries and their relationships.
$$R(q_i,d_j)$$ is a ranking function which associates a real number with a query $$q_i \in Q$$ and a document representation $$d_j \in D$$. Such ranking defines an ordering among the documents with regard to the query $$q_i$$.
Section 2.5.1 Basic Concepts of Classic IR
Each document is described by a set of representative key workds calle index terms.
- Index terms are usually nouns. Why? Because verbs, adjectives connectives etc. have little meaning on their own.
- Index terms have weights described as follows:
Definition Let $$t$$ be the number of index terms in the system and $$k_i$$ be a generic index term. $$K={k_1,...,k_t}$$ is the set of all index terms. A weight $$w_{i,j} > 0$$ is associated with each index term $$k_i$$ of a document $$d_j$$. For an index term which does not appear in the document text, $$w_{i,j}=0$$. With document $$d_j$$ is associated an index term vector $$\vec{d}_{j}=(w_{1,j},w_{2,j},...,w_{t,j})$$. Further, let $$g_{i}$$ be a function that returns the weight associated with the index term $$k_{i}$$ in any $$t$$-dimensional vector (i.e., $$g_{i}(\vec{d}_{j})=w_{i,j}$$).
Section 2.5.2 Boolean Model
- index terms are weighted either 0 or 1.
Queries are expressed in DisjunctiveNormalForm of the $$[q=k_{a}\wedge (k_{b}\vee \lnot k_{c})]$$ can be written in disjunctive
normal form as $$[\vec{q}_{dnf}=(1,1,1)\vee (1,1,0)\vee (1,0,0)]$$.
Definition For the Boolean model, the index term weight variables are all binary ie.e, $$w_{i,j} \in {0,1}$$. A query $$q$$ is a conventional boolean expression. Let $$\vec{q}_{dnf}$$ be the disjunctive normal form for the query $$q$$. further, let $$\vec{q}_{cc}$$ be any of the conjunctive components of $$\vec{q}_{dnf}$$. The similarity of a document $$d_j$$ to the query $$q$$ is defined as
$$sim(d_{j},q)= \left\{\begin{array}{ll} 1 & if~\exists \vec{q}_{cc}~|~(\vec{q}_{cc}\in \vec{q}_{dnf})\wedge (\forall k_{i},g_{i}(\vec{d}_{j})=g_{i}(\vec{q}_{cc}) \\ 0 & otherwise \end{array} \right.$$
If $$sim(d_j,q)=1$$ then the Boolean model predicts that the document $$d_j$$ is relevant to the query $$q$$ (it might not be). Otherwise, the prediction is that the document is not relevant.
Section 2.5.3 Vector Model
- Weights are non-binary that is real numbers
- This allows us to calculate a degree of similarity.
Definition For the vector model, the weight $w_{i,j}$ associated with a pair $$(k_{i},j_{j})$$ is positive and non-binary. Further, the index terms in the query are also weighted. Let $w_{i,q}$ be the weight associated with the pair $$[k_{i},q]$$, where $$w_{i,q}\ge q0$$. Then, the query vector $$\vec{q}$$ is defined as $$\vec{q}=(w_{1,q},...,w_{t,q})$$ where $$t$$ is the total number of index terms in the system. As before, the vector for a document $$d_{j}$$ is represented by $$\vec{d}_{j}=(w_{1,j},...,w_{t,j})$$.
Thus we have a document $$d_{j}$$ and user query $$q$$ represented as $$t$$-dimensional vectors. Similarity is defined cosine of the angle between the document vector and the query vector as follows:
attachment:csce810_2_2.png
Figure 2
Having defined similarity the we now have a method for ranking and we can determine what is relevant by setting a threshold on the degree of similarity. This is essentially a clustering algorithm that clusters documents similar to the query in one set and documents dissimilar to the query in the other set. We say the IR problem can be reduced to a clustering problem determining what documents belong to the relevant set A and which do not. There are two main issues to resolved in a clustering problem:
intra-cluster similarity --> term frequency (tf): One needs to determine what are the features which better describe the objects in set A.
intra-cluster dissimilarity --> inverse document frequency (idf): One needs to determine what are the features which better distinguish the objects in set A from the remaining objects in collection C (the set of all documents).
Definition
Let $$N$$ be the total number of documents in the system and $$n_i$$ be the number of documents in which the index term $$k_i$$ appears. Let $$freq_{i,j}$$ be the raw frequency of term $$k_i$$ in the document $$d_j$$ (i.e., the number of times the term $k_i$ is mentioned in the text of the document $d_j$). Then, the {\bf normalized} frequency $f_{i,j}$ of term $k_i$ in document $d_j$ is given by:
$$$f_{i,j}=\frac{freq_{i,j}}{\max_{l}(freq_{l,j})}$$$
where the maximum is computed over all terms which are mentioned in the text of the document $$d_j$$. If the term $$k_i$$ does not appear in the document $$d_j$$ then $$f_{i,j}=0$$. Further, let $$idf_i$$, inverse document frequency for $$k_i$$ given by:
$$$idf_{i,j}=\log\frac{N}{n_{i}}$$$
The best known term weighting schemes use weights which are given by
$$$w_{i,j}=f_{i,j}\times\log\frac{N}{n_{i}}$$$
or by a variation of this formula. Such term-weighting strategies are called $$tf$$-$$idf$$ schemes.
One such term wights formula was given by Salton and Buckley as
$$$w_{i,q}=\left( 0.5+\frac{0.5~freq_{i,q}}{\max_{l}\left( freq_{l,q}\right)}\right) \times\log\frac{N}{n_{i}}$$$
Advantages
- Term-weighting scheme improves retrieval performance
- Partial matching allows retrieval of documents that approximate the query conditions
- The cosine ranking formula sorts the documents according th their degree of similarity
Disadvantages
- Does not account for term dependencies
- Answer sets are difficult to improve without query expansion or relevance feedback.
Section 2.5.4 Probabilistic Model
Main Idea: Given a user query there is a set of documents which contains exactly the relevant documents and no other.
- There exists an ideal answer set to a query.
Given a set of index terms we guess at the properties of the ideal set and retrieve that set. This becomes the guess or initial set of documents.
Assumption (Prababilistic Principle):
Given a user query $$q$$ and a document $$d_{j}$$ in the collection, the probabilistic model tries to estimate the probability that the user will find teh document interesting (i.e. relevant). The model assumes that this probability of relevance depends on the query and the document representations only. Further, the model assumes that there is a subset of all documents which the user prefers as the answer set for the query $$q$$. Such an ideal answer set is labeled $$R$$ and should maximized the overall probability of relevance to the user. Documents in the set $$R$$ are predicted to be relevant to the query. Documents not in this set are predicted to be non-relevant.
Given a query $$q$$, the probabilistic model assigns to each document $$d_{j}$$, as a measure of its similarity to the query, the ratio:
$$$sim(d_{j},q) = \frac{P(d_{j}~relevant-to~q)}{P(d_{j}~non-relevant-to~q)}$$$
which computes the odds of the document $$d_{j}$$ being relevant to the query $$q$$. Taking the odds of relevance as the rank minimizes the probability of an erroneous judgement.
Definition
For the probabilistic mode, the index term weight variables are all binary i.e., $$w_{i,j} \in{0,1}$$, $$w_{i,q} \in{0,1}$$. A query $$q$$ is a subset of index terms. Let $$R$$ be the set of documents known (or initially guessed}) to be relevant. Let $$\bar{R}$$ be the complement of $$R$$ (i.e. the set of initially guessed non-relevant documents). Let $$P(R|\vec{d}_{j})$$ be the probability that the document $$d_{j}$$ is relevant to the query $$q$$ and $$P(\bar{R}|\vec{d_{j}}$$ be the probability that $$d_{j}$$ is non-relevant to $$q$$. The similarity $$sim(d_{j},q)$$ of the document $$d_{j}$$ to the query $q$ is defined as the ratio:
$$$sim(d_{j},q) = \frac{ P(R|\vec{d_{j}}) }{ P(\bar{R}|\vec{d}_{j}) }$$$
Using Bayes' rule, \begin{equation} sim(d_{j},q) = \frac{ P(\vec{d_{j}}|R) \times P(R) }{ P(\vec{d}_{j}|\bar{R}) \times P(\bar{R}) }% \end{equation} For more info see P32 MIR. They assume that $P(R)$ and $P(\bar{R})$ are the same for all the documents in the collection. This doesn't make sense to me unless we assume that about $50\%$ of the documents that are relevant. The other option is to say that a few are definitely relevant and a few are definitely irrelevant, and the rest are in a different category of quasi-relevant. Even this doesn't make sense though because we named the two sets $R$ and $\bar{R}$. Big question!
If we leave off $R$ and $\bar{R}$ we get: \begin{equation} sim(d_{j},q)~\symbol{126}~\frac{P(\vec{d_{j}}|R)}{P(\vec{d}_{j}|\bar{R})}% \end{equation} Assuming independence of index terms, \begin{equation} sim(d_{j},q)~\symbol{126}~\frac{\left( \prod_{g_{i}(\vec{d}_{j})=1}% P(k_{i}|R))\right) \times\left( \prod_{g_{i}(\vec{d}_{j})=0}P\left( \bar {k}_{i}|R\right) \right) }{\left( \prod_{g_{i}(\vec{d}_{j})=1}P\left( k_{i}|\bar{R}\right) \right) \times\left( \prod_{g_{i}(\vec{d}_{j}% )=0}P\left( \bar{k}_{i}|\bar{R}\right) \right) }% \label{eq:ProbabilitySimRelation1}% \end{equation} where: $g_{i}(\vec{d}_{j})=1$ means the weight of query keyword $\left( g_{i}(\vec{d}_{i})=k_{i}\right) $of document $d_{j}$ is $1$ and $P\left( k_{i}|R\right) $ stands for the probability that the index term $k_{i}$ is present in a document reandomly selected from the set $R$. $P\left( \bar {k}_{i}|R\right) $ stands for the probability that the index term $k_{i}$ is not present in a document randomely selected from the set $R$. And of course $R$ is the initial guess at the relevant set. With some massaging of (\ref{eq:ProbabilitySimRelation1}) we can get:% \begin{equation} sim\left( d_{j},q\right) ~\symbol{126}~\sum_{i=1}^{t}w_{i,q}\times w_{i,j}\times\left( \log\frac{P\left( k_{i}|R\right) }{1-P\left( k_{i}|R\right) }+\log\frac{1-P\left( k_{i}|\bar{R}\right) }{P\left( k_{i}|\bar{R}\right) }\right) \label{eq:ProbabilitySimRelation2}% \end{equation}
\end{definition}
In the very beginning (i.e. immediately after the query specification), there are no retrieved documents. Thus, one has to make simplifying assumptions such as
\begin{enumerate} \item assume that $P\left( k_{i}|R\right) $ is constant for all index terms $k_{i}\in q$
\item assume that the distribution of index terms among the non-relevant documents can be approximated by the distribution of index terms among all the docuemnts in the collection. \ \end{enumerate}
From these two assumptions we get:% \begin{align} P\left( k_{i}|R\right) & =0.5\\ P\left( k_{i}|\bar{R}\right) & =\frac{n_{i}}{N}% \end{align} where $n_{i}$ is the number of documents that contain the keyword $k_{i}$ and $N$ is the total number of documents in the collection. Now that we have initial values for the probabilities we can use (\ref{eq:ProbabilitySimRelation2}) to rank the documents and determine our first guess at the set of document that belong in $R$ call this initial set $V$ determined by the top $r$ ranked documents. Define $V_{i}$ to be the subset of $V$ containing keyword $k_{i}$. Now we are ready to improve our guesses for $P\left( k_{i}|R\right) $ and $P\left( k_{i}|\bar{R}\right) $. We accomplish this with the following assumptions
\begin{enumerate} \item We can approximate $P\left( k_{i}|R\right) $ by the distribution of index term $k_{i}$ among the documents retrieved so far
\item We can approximate $P\left( k_{i}|\bar{R}\right) $ by considering all the non-retrieved documents as not relevant. \end{enumerate}
From these two assumptions we get:% \begin{align} P\left( k_{i}|R\right) & =\frac{\left\vert V_{i}\right\vert }{\left\vert V\right\vert }\\ P\left( k_{i}|\bar{R}\right) & =\frac{n_{i}-\left\vert V_{i}\right\vert }{N-\left\vert V\right\vert }% \end{align} This process can be repeated without any human intervention to improve our guesses for the probabilites. For small values of $\left\vert V_{i}\right\vert $ we in practice make the above two equations:% \begin{align} P\left( k_{i}|R\right) & =\frac{\left\vert V_{i}\right\vert +0.5}% {\left\vert V\right\vert }\\ P\left( k_{i}|\bar{R}\right) & =\frac{n_{i}-\left\vert V_{i}\right\vert +0.5}{N-\left\vert V\right\vert }% \end{align} or \begin{align} P\left( k_{i}|R\right) & =\frac{\left\vert V_{i}\right\vert +\frac{n_{i}% }{N}}{\left\vert V\right\vert }\\ P\left( k_{i}|\bar{R}\right) & =\frac{n_{i}-\left\vert V_{i}\right\vert +\frac{n_{i}}{N}}{N-\left\vert V\right\vert }% \end{align}
}}}
